模数转换器 (ADC)
最新课程
- 电源培训授证项目-在线答疑Q&A 直播回放
- 高压 MOSFET/IGBT 栅极驱动原理与设计 (下)
- 高压 MOSFET/IGBT 栅极驱动原理与设计 (上)
- C2000™ Σ-Δ 滤波器调制器 (SDFM)
- C2000™ 的传感和处理功能
- C2000™ 可配置逻辑块 (CLB)
- C2000™ 模数转换器 (ADC) 培训
- C2000™ 增强型脉宽调制器 (ePWM)
- Code Composer Studio™ 快速提示
- 用于优化电源性能的 PCB 布局指南
热门课程
10.7 高速数据转换器信号处理:真实和复杂的调制
大家好,欢迎观看 该演示,其中讨论
实调制和复调制。
在本视频中, 我们将首先
讨论什么是调制以及 一些常见类型的调制。
然后我们将深入 探究相位和振幅
调制及其背后的 数学原理,从而
介绍实调制和 复调制的概念。
最后,我们将讨论 复调制的用法并
介绍一个将这些概念 联系在一起的示例。
首先,让我们来 讨论基本调制。
调制是以受控 方式更改载波
信号的振幅、 相位或频率等
属性,从而在 通道上传输
数据或获取所需 信号属性的操作。
此处针对一个数字 通信系统展示了
该过程。
我们具有一个用于 控制调制器的位序列。
该调制器会响应 每个位或位序列,
从而以特定的 方式调制信号,
以表示这些位。
信号在通道上 传输,该通道
可能是同轴 电缆、无线通道
或光纤。
在传输之后, 经调制的
信号会进行 解调,以显示
传输的位。
所使用的 调制技术
有很多类型。
每种类型的调制 都可以在频谱效率、
复杂性、功效、 抗噪性能等
方面实现不同的折衷。
此处提供了一些 最常使用的调制
类型。
脉冲振幅 调制,称为 PAM,
仅调制 载波振幅。
PAM 也可以 包含负振幅,
可以将其视为 180 度的相移。
例如,2 级 PAM, 通常称为二进制
相移键控或 BPSK,常用于
千兆位 以太网等
串行化接口。
当然,最著名的 模拟振幅调制
是在 AM 无线电 传输中使用的调制。
相移键控,或 PSK, 仅调制载波相位,
这将产生能够 实现出色功效的
恒定载波包络。
PSK 具有出色的 抗噪性能,当通道
具有低信噪比时 用于 LTE 网络,以实现
足够的 误码率。
正交振幅 调制,称为 QAM,
调制载波 相位和振幅,
从而允许使用 大量的符号来
极大地提高 频谱效率,
但代价是降低功效 并且产生更多不同的
噪声要求。
这是当今最常使用的 调制类型之一。
DOCSIS 3.0 电缆系统中 使用 256 符号 QAM,以
在低噪声通道上 实现高数据速率。
频率调制调制 载波频率。
在数字通信中, 选择离散频率
作为符号,每个 符号表示一个
位序列。
当然,其他示例 包括 FM 无线电
和线性频率 调制或 LFM。
LFM 是对载波频率的 连续线性扫描。
LFM 通常不用于 数据传输。
不过,它用于 雷达系统,以
实现脉冲压缩, 这可以提高空间
分辨率,从而 能够识别间距
很小的物体。
现在,让我们来看看 基本相位和振幅调制
背后的数学原理。
这是一个很好的 示例,因为它
被广泛使用, 如正交振幅
调制或 QAM。
该同一基本分析 可用于前一张
幻灯片中提供的 所有调制类型。
我们还可以 利用它来说明
实调制和复调制。
首先,相位和振幅 调制载波可以
如此处所示 进行表示,
其中余弦项 用作载波,该
载波的振幅以 a(t) 进行 调制,相位以 θt 进行调制。
载波频率 表示为 fc。
通过使用角度 之和三角恒等式,
我们可以将 x(t) 分解为单独的
正弦和余弦载波, 每个载波的振幅
都调制为 a(t), 相位调制为
相位调制函数 θt 的 相应正弦和余弦。
然后,我们可以 为每个载波函数
重新定义振幅和 相位,它们分别称为
xi(t) 和 xq(t)。
这些调制函数 通常简单地称为
I 和 Q。i 是 同相调制函数,
q 是正交相位 调制函数。
正交项来自 彼此具有 90
度相位差的 正弦和余弦。
我们现在具有该形式的 x(t),这表示我们的真实
传输信号。
I 和 Q 调制 函数是实
值函数,这 意味着它们
不包含虚部。
因此,x(t) 是 实值函数,
它是真实传输 所需要的。
不过,该函数 实际上可以
表示实调制 和复调制。
简而言之, 该传输信号
通常称为 带通信号,
因为它在某个载波 频率上占据了一些带宽。
或者换句话说, I 和 Q 函数调制
载波信号。
带通信号 可以分解为
带通调制 函数乘以
复指数载波。
术语“低通”指在 直流上作为中心的
信号,也称为基带。
该新的基带 调制函数 Xbb(t)
由 I 和 Q 实值 调制函数构成,
其中 Q 表示 复数分量。
很容易看到, 如果 fq(t) 等于
0,那么 Xbb(t) 是实值函数。
当 Xbb(t) 是 实值时,
结果为实调制。
或者,如果 Xbb(t) 不是零,
那么它是会导致 复调制的复信号。
我们现在 可以将该新的
复基带调制 函数重新与
实值带通传输信号 相关联,如此处所示。
可以通过将 Xbb(t) 乘以一个
复指数来求解 x(t),其中频率
等于载波频率,并且 采用该乘积的实部。
我们将该形式的 传输信号称为
分析等效,因为 其主要目的是
分析调制。
使用欧拉 公式和 Xbb(t) 的
定义,很容易 看到该 x(t)
定义等效于 前面的定义。
您可以尝试自己 说明该等效性。
说到底,Xbb(t) 就是一个随
时间变化的 复数,该复数受
I 和 Q 调制 函数控制。
请记住,I 和 Q 是实值函数,
Xbb(t) 仅在 q 函数不是零时
才是复数。
接下来,我们将 说明与实调制
相比,使用 复调制的优势。
此处是一个 实调制示例,
其中采用一个 余弦波并将其
转换为更高的频率。
我们通常将该过程 称为混合,但可以
将其视为使用 一个正弦波来
调制另一个正弦波。
在这种情况下,基带 调制函数是一个
针对所有时间值 都是实值的余弦波。
或者换句话说, q 分量为零。
基带余弦 波的频率
是 fIF,其中 IF 表示中频。
针对某个余弦 使用欧拉关系,
我们可以将该 余弦描述为两个
复指数的和。
将这插入到 x(t) 的分析定义中,
合并指数幂,然后 使用欧拉公式,
我们可以看到 生成的调制信号
是载波频率加减 IF 频率下的两个
实余弦波之和。
不过,通常只有其中 一个信号是我们
需要的,不需要的 信号称为像,
必须将其滤除。
解决该问题的一种 方法是使用复调制。
因此考虑 相同的情形,
但使用复调制。
在这里,基带 调制函数是
一个复指数, 而不是实值
余弦波。
再次使用欧拉 公式,我们可以
看到复指数就是一个 余弦和一个正弦之和,
其中正弦项乘以 j。
因此同相调制 函数或 I 是一个
余弦波,正交 相位调制函数
或 q 是一个正弦波。
将该复基带 函数插入到
x(t) 的分析 定义中,
合并指数幂,然后使用 欧拉公式,可以得到
最终的调制信号。
实部函数 删除了正弦
虚部。
该新的调制 信号仅包含
所需的信号, 像信号得到
衰减或抑制。
让我们尝试将 该示例在频域中
可视化。
在实混合 情况中,
首先要明白的是, 余弦波等实信号
具有镜像的 正负频谱。
负频率在真实世界中 是不存在的,但存在于
分析世界中。
实调制信号具有 相同的情况,
如该图形所示。
请注意,正负 频谱看起来
是一样的。
当该信号混合至 更高的频率时,
正负频谱 混合至
载波频率。
我们将载波 频率的两端
称为下边带 和上边带。
在这种情况下, 下边带和上边带
包含相同的信息, 效率并不是很高。
该情形称为 双边带或
DSB 传输,这是 实调制的
结果。
如果我们现在 看看复混合情况,
其中我们使用了 复指数作为基带
信号,那么我们 可以看到复正弦
仅存在于正 频率空间中,
负像消失了。
我还可以将 复指数定义为
负频率,这意味着 它存在于负频率
空间中,而不 存在于正频率
空间中。
这说明我的 正频率空间
独立于我的 负频率空间。
如该图形所示, 我的复调制信号
可以在两个 边带中包含
不同的信息。
在我将其与 复正弦混合
并获取实部 之后,载波
信号的下边带 和上边带现在
是独立的。
这称为单边带 传输或 SSB,
因为每个边带可以 传输独特的信息。
主要的优势是, 与实传输相比,
这使我 可以通过
相同的带宽传输 两倍的信息量。
现在我们已经介绍了复调制 背后的基本数学原理,那么
让我们来讨论两种主要的用法。
首先,复调制 概念用于
像抑制混频器, 其中实混合会
产生需要的 信号和不需要的
像信号,必须 将该像信号
滤除。
正如我在复混合 示例中展示的那样,
通过使用复调制,可以 实现固有的像信号抑制。
像信号抑制可以 降低混频器后面的
模拟滤波器要求。
由于存在一些缺陷, 模拟混频器无法
实现完美的抑制,
不过,即使像信号 功率降低 20dB,
也会极大地 降低滤波器
要求。
其次,复调制 广泛用于数字
通信,以针对 给定的信号
带宽将数据 速率加倍。
这可以提高频谱 效率,这一点在带宽
受限时非常重要,例如 在进行无线通信时。
数据速率加倍 是可以实现的,
因为正弦和 余弦是正交
函数,从而可以 分离 I 和 Q 分量。
由于 I 和 Q 可以分离,因此
它们可以包含 独立的信息。
让我们更详细地 看看该用例。
数字通信使用 离散的 I 和 Q 值
来形成符号。
使复符号 可视化的
一种常见方法 是使用星座图,
例如该用于 16 QAM 的示例图。
该图将符号 映射到复平面。
x 轴表示 实部 I 的
幅度,而 y 轴表示虚部
Q 的幅度。
每个符号 都映射到
一个位序列, 以传输信息。
在该示例图中, 位序列 1011 映射
右下角的符号, 由最大正 I 值
和最小负 Q 值表示。
原始值与符号 之间的距离
表示调制 载波振幅,
可以使用勾股 定理进行计算。
调制载波的 相位是正 I 轴
与符号之间的 夹角,可以使用
q/i 的反正切 进行计算。
现在,让我们 尝试连接
星座图中 显示的内容
与前面显示的传输 信号定义之间的点。
首先,考虑前面 显示的 16 QAM
星座图。
假设我们希望 在通道上以载波
频率 fc 进行传输, 并且我们希望发送
位 0011。
查看该图,我们 可以看到位 0011
被分配至复平面 右下角象限中的
左下角符号。
该符号分别对应 I 和 Q 值 1 和 负
3。
因此我们的基带调制 函数就是简单的 1 减 j3。
现在我们可以 使用前一张
幻灯片中的公式计算 载波振幅和相位。
我们发现振幅 是 10 的平方根,
相位是负 1.25 弧度。
现在我们可以通过两种 方法生成调制信号。
我们可以使用 计算的振幅和
相位来设置余弦 波的振幅和相位,
如顶部的公式所示。
或者,我们可以 直接使用星座图
中的 I 和 Q 值来 设置独立的余弦项
和正弦项的 相对振幅,
如底部公式所示。
生成的信号 是相同的。
不过,第二种方法 是通常使用的方法,
因为它更易于在数字 处理器或 FPGA 中实现。
这里是一些 用于各种调制
方案的星座图。
第一个是正交 相移键控或
QPSK,它具有 四个符号,
复平面的每个 象限中一个。
第二个是八符号 相移键控或
8PSK,,它具有 八个符号,
相邻符号间距为 45 度。
第三个是 32 QAM,它没有
形成一个完美的正方形, 因为 32 的平方根
不是一个整数。
相反,该正方形的 四个角被移除了,
这可以稍微 提高功效,
并允许向每个 符号映射五个位。
最后一个是 1,024 QAM, 它是非常紧凑的星座,
向每个符号映射 10 个 位,从而极大地提高
数据速率。
很容易看到, 由于紧密排列的
符号,星座越稠密, 所需要的噪声和
失真性能就越高, 以实现相同的
误码率。
不过,对于符号之间 距离较远的星座,
每个符号发送的 位数也较少,因此
具有较低的数据速率。
许多系统允许 在通道条件改善
或变差时动态 改变星座,以
针对所需的 误码率实现
最高的数据速率。
本视频到此结束。
谢谢观看。 348
-
 未学习 1.1 数据转换器介绍 - 直流参数
未学习 1.1 数据转换器介绍 - 直流参数
-
 未学习 1.2 数据转换器介绍 - 交流和直流参数
未学习 1.2 数据转换器介绍 - 交流和直流参数
-
 未学习 2.1 数据转换器介绍 - SAR型ADC输入类型
未学习 2.1 数据转换器介绍 - SAR型ADC输入类型
-
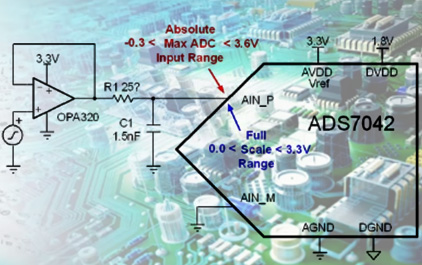 未学习 2.2.1 单端驱动电路分析
未学习 2.2.1 单端驱动电路分析
-
 未学习 2.2.2 反向配置与轨对轨放大器的交越失真
未学习 2.2.2 反向配置与轨对轨放大器的交越失真
-
 未学习 2.3.1 交越失真实验所需硬件软件
未学习 2.3.1 交越失真实验所需硬件软件
-
 未学习 2.3.2 交越失真实验软件设置
未学习 2.3.2 交越失真实验软件设置
-
 未学习 2.3.3 交越失真实验结果
未学习 2.3.3 交越失真实验结果
-
 未学习 2.4.1 仪表放大器输入范围计算
未学习 2.4.1 仪表放大器输入范围计算
-
 未学习 2.4.2 使用软件验证仪表放大器输入共模范围
未学习 2.4.2 使用软件验证仪表放大器输入共模范围
-
 未学习 2.5.1 全差分放大器及失真
未学习 2.5.1 全差分放大器及失真
-
 未学习 2.5.2 全差分驱动电路设计
未学习 2.5.2 全差分驱动电路设计
-
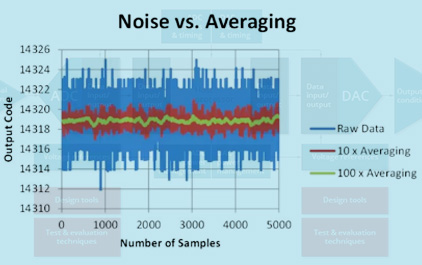 未学习 3.1 误差分析背后的统计学知识
未学习 3.1 误差分析背后的统计学知识
-
 未学习 3.2 理解与校准ADC系统的偏移和增益误差
未学习 3.2 理解与校准ADC系统的偏移和增益误差
-
 未学习 3.3 使用蒙特卡罗SPICE工具进行误差统计分析
未学习 3.3 使用蒙特卡罗SPICE工具进行误差统计分析
-
 未学习 4.1 计算ADC系统的总噪声
未学习 4.1 计算ADC系统的总噪声
-
 未学习 4.2 动手实验-ADC噪声
未学习 4.2 动手实验-ADC噪声
-
 未学习 4.3 ADC 系统中的噪声
未学习 4.3 ADC 系统中的噪声
-
 未学习 4.4 ADC 噪声测量、方法和参数
未学习 4.4 ADC 噪声测量、方法和参数
-
 未学习 4.5 低速 Δ-Σ ADC 的系统噪声性能
未学习 4.5 低速 Δ-Σ ADC 的系统噪声性能
-
 未学习 4.6 分析和计算 ADC 系统中的噪声带宽——多级滤波器
未学习 4.6 分析和计算 ADC 系统中的噪声带宽——多级滤波器
-
 未学习 4.7 分析和计算 ADC 系统中的噪声带宽——数字滤波器
未学习 4.7 分析和计算 ADC 系统中的噪声带宽——数字滤波器
-
 未学习 4.8 增益对噪声、ADC FSR 和动态范围的影响
未学习 4.8 增益对噪声、ADC FSR 和动态范围的影响
-
 未学习 4.9 计算放大器 + ADC 总噪声:设计示例
未学习 4.9 计算放大器 + ADC 总噪声:设计示例
-
 未学习 4.10 ADC 系统中的参考噪声简介
未学习 4.10 ADC 系统中的参考噪声简介
-
 未学习 4.11 参考噪声对信号链性能的影响
未学习 4.11 参考噪声对信号链性能的影响
-
 未学习 4.12 降低参考噪声
未学习 4.12 降低参考噪声
-
 未学习 5.1 频域介绍
未学习 5.1 频域介绍
-
 未学习 5.2 快速傅立叶变换及加窗函数
未学习 5.2 快速傅立叶变换及加窗函数
-
 未学习 5.3 改善频率指标的方法:相干采样及滤波
未学习 5.3 改善频率指标的方法:相干采样及滤波
-
 未学习 5.4 混叠及抗混叠滤波器
未学习 5.4 混叠及抗混叠滤波器
-
 未学习 5.5 实验 - 混叠和抗混叠滤波器
未学习 5.5 实验 - 混叠和抗混叠滤波器
-
 未学习 6.1 SAR ADC及其器件选型
未学习 6.1 SAR ADC及其器件选型
-
 未学习 6.2 驱动放大器的选型和验证
未学习 6.2 驱动放大器的选型和验证
-
 未学习 6.3 建立SAR ADC的仿真模型
未学习 6.3 建立SAR ADC的仿真模型
-
 未学习 6.4 如何计算RC滤波器的值
未学习 6.4 如何计算RC滤波器的值
-
 未学习 6.5 最终的仿真验证
未学习 6.5 最终的仿真验证
-
 未学习 6.6 滤波器RC选型的理论计算方法
未学习 6.6 滤波器RC选型的理论计算方法
-
 未学习 6.7 R-C组件选择背后的数学
未学习 6.7 R-C组件选择背后的数学
-
 未学习 7.1 电压基准概述
未学习 7.1 电压基准概述
-
 未学习 7.2 参考驱动器拓扑概述
未学习 7.2 参考驱动器拓扑概述
-
 未学习 7.3 了解SAR参考输入模型
未学习 7.3 了解SAR参考输入模型
-
 未学习 7.4 开发SAR输入参考模型
未学习 7.4 开发SAR输入参考模型
-
 未学习 7.5 驱动参考实验
未学习 7.5 驱动参考实验
-
 未学习 7.6 ADC:SAR 基准输入 - CDAC
未学习 7.6 ADC:SAR 基准输入 - CDAC
-
 未学习 8.1 SAR ADC功率调节
未学习 8.1 SAR ADC功率调节
-
 未学习 8.2 动手实验 - 系统功率调节
未学习 8.2 动手实验 - 系统功率调节
-
 未学习 9.1 EOS和ESD
未学习 9.1 EOS和ESD
-
 未学习 9.3 向TINA 导入二极管PSpice模型
未学习 9.3 向TINA 导入二极管PSpice模型
-
 未学习 9.4 通过高压放大器保护低压ADC
未学习 9.4 通过高压放大器保护低压ADC
-
 未学习 9.5 保护低压ADC-改进的解决方案
未学习 9.5 保护低压ADC-改进的解决方案
-
 未学习 9.6 用TVS二极管保护ADC
未学习 9.6 用TVS二极管保护ADC
-
 未学习 9.7 用TVS二极管保护ADC –改进的解决方案
未学习 9.7 用TVS二极管保护ADC –改进的解决方案
-
 未学习 10.1 了解和比较高速模数(ADC)和数模转换器(DAC)转换器架构
未学习 10.1 了解和比较高速模数(ADC)和数模转换器(DAC)转换器架构
-
 未学习 10.2 抖动对高速模数转换器(ADC)信噪比(SNR)的影响
未学习 10.2 抖动对高速模数转换器(ADC)信噪比(SNR)的影响
-
 未学习 10.3了解高速数据转换器中的信噪比(SNR)和噪声频谱密度(NSD)
未学习 10.3了解高速数据转换器中的信噪比(SNR)和噪声频谱密度(NSD)
-
 未学习 10.4 带宽与频率 - 子采样概念
未学习 10.4 带宽与频率 - 子采样概念
-
 未学习 10.5 高速数据转换器中的采样率与数据速率,抽取(DDC)和插值(DUC)概念
未学习 10.5 高速数据转换器中的采样率与数据速率,抽取(DDC)和插值(DUC)概念
-
 未学习 10.6 频率和采样率规划:了解高速ADC中的采样,奈奎斯特区,谐波和杂散性能
未学习 10.6 频率和采样率规划:了解高速ADC中的采样,奈奎斯特区,谐波和杂散性能
-
 未学习 10.7 高速数据转换器信号处理:真实和复杂的调制
未学习 10.7 高速数据转换器信号处理:真实和复杂的调制
-
 未学习 (中文)11.1 ADC 系统中的噪声
未学习 (中文)11.1 ADC 系统中的噪声
-
 未学习 (中文)11.3 ADC 噪声测量、方法和参数
未学习 (中文)11.3 ADC 噪声测量、方法和参数
-
 未学习 (中文)11.4 低速 Δ-Σ ADC 的系统噪声性能
未学习 (中文)11.4 低速 Δ-Σ ADC 的系统噪声性能
-
 未学习 (中文)11.5 分析和计算 ADC 系统中的噪声带宽——多级滤波器
未学习 (中文)11.5 分析和计算 ADC 系统中的噪声带宽——多级滤波器
-
 未学习 (中文)11.6 分析和计算 ADC 系统中的噪声带宽——数字滤波器
未学习 (中文)11.6 分析和计算 ADC 系统中的噪声带宽——数字滤波器
-
 未学习 (中文)11.7 增益对噪声、ADC FSR 和动态范围的影响
未学习 (中文)11.7 增益对噪声、ADC FSR 和动态范围的影响
-
 未学习 (中文)11.8 计算放大器 + ADC 总噪声:设计示例
未学习 (中文)11.8 计算放大器 + ADC 总噪声:设计示例
-
 未学习 (中文)11.9 ADC 系统中的参考噪声简介
未学习 (中文)11.9 ADC 系统中的参考噪声简介
-
 未学习 (中文)11.10 参考噪声对信号链性能的影响
未学习 (中文)11.10 参考噪声对信号链性能的影响
-
 未学习 (中文)11.11 降低参考噪声
未学习 (中文)11.11 降低参考噪声
-
 未学习 动手实验:放大器稳定和电荷桶滤波器设计
未学习 动手实验:放大器稳定和电荷桶滤波器设计
-
 未学习 无需放大器即可驱动 SAR ADC
未学习 无需放大器即可驱动 SAR ADC
-
 未学习 外部EOS保护装置
未学习 外部EOS保护装置
-
 未学习 (中文)5.5 实验 - 混叠和抗混叠滤波器
未学习 (中文)5.5 实验 - 混叠和抗混叠滤波器
-
 未学习 (中文)6.7 R-C组件选择背后的数学
未学习 (中文)6.7 R-C组件选择背后的数学
-
 未学习 (中文)7.1 电压基准概述
未学习 (中文)7.1 电压基准概述
-
 未学习 (中文)7.3 SAR 基准输入 - CDAC
未学习 (中文)7.3 SAR 基准输入 - CDAC
-
 未学习 (中文)7.4 了解SAR参考输入模型
未学习 (中文)7.4 了解SAR参考输入模型
-
 未学习 (中文)7.5 开发SAR输入参考模型
未学习 (中文)7.5 开发SAR输入参考模型
-
 未学习 (中文)7.6 驱动参考实验
未学习 (中文)7.6 驱动参考实验
-
 未学习 (中文)8.1 SAR ADC功率调节
未学习 (中文)8.1 SAR ADC功率调节
-
 未学习 (中文)8.2 动手实验 - 系统功率调节
未学习 (中文)8.2 动手实验 - 系统功率调节
-
 未学习 (中文)9.1 EOS和ESD
未学习 (中文)9.1 EOS和ESD
-
 未学习 (中文)9.3 向TINA 导入二极管PSpice模型
未学习 (中文)9.3 向TINA 导入二极管PSpice模型
-
 未学习 (中文)9.4 通过高压放大器保护低压ADC
未学习 (中文)9.4 通过高压放大器保护低压ADC
-
 未学习 (中文)9.5 保护低压ADC-改进的解决方案
未学习 (中文)9.5 保护低压ADC-改进的解决方案
-
 未学习 (中文)9.6 用TVS二极管保护ADC
未学习 (中文)9.6 用TVS二极管保护ADC
-
 未学习 (中文)9.7 用TVS二极管保护ADC –改进的解决方案
未学习 (中文)9.7 用TVS二极管保护ADC –改进的解决方案
-
 未学习 (中文)10.1 了解和比较高速模数(ADC)和数模转换器(DAC)转换器架构
未学习 (中文)10.1 了解和比较高速模数(ADC)和数模转换器(DAC)转换器架构
-
 未学习 (中文)10.2 抖动对高速模数转换器(ADC)信噪比(SNR)的影响
未学习 (中文)10.2 抖动对高速模数转换器(ADC)信噪比(SNR)的影响
-
 未学习 (中文)10.3 了解高速数据转换器中的信噪比(SNR)和噪声频谱密度(NSD)
未学习 (中文)10.3 了解高速数据转换器中的信噪比(SNR)和噪声频谱密度(NSD)
-
 未学习 (中文)10.4 带宽与频率 - 子采样概念
未学习 (中文)10.4 带宽与频率 - 子采样概念
-
 未学习 (中文)10.5 高速数据转换器中的采样率与数据速率,抽取(DDC)和插值(DUC)概念
未学习 (中文)10.5 高速数据转换器中的采样率与数据速率,抽取(DDC)和插值(DUC)概念
-
 未学习 (中文)10.6 频率和采样率规划:了解高速ADC中的采样,奈奎斯特区,谐波和杂散性能
未学习 (中文)10.6 频率和采样率规划:了解高速ADC中的采样,奈奎斯特区,谐波和杂散性能
-
 未学习 (中文)10.7 高速数据转换器信号处理:真实和复杂的调制
未学习 (中文)10.7 高速数据转换器信号处理:真实和复杂的调制
-
 未学习 (中文)了解 ADC 系统中的电源噪声
未学习 (中文)了解 ADC 系统中的电源噪声
-
 未学习 (中文)时钟噪声如何影响精密 ADC 测量
未学习 (中文)时钟噪声如何影响精密 ADC 测量
-
 未学习 (中文)电源噪声降低技术
未学习 (中文)电源噪声降低技术