模数转换器 (ADC)
最新课程
- 电源培训授证项目-在线答疑Q&A 直播回放
- 高压 MOSFET/IGBT 栅极驱动原理与设计 (下)
- 高压 MOSFET/IGBT 栅极驱动原理与设计 (上)
- C2000™ Σ-Δ 滤波器调制器 (SDFM)
- C2000™ 的传感和处理功能
- C2000™ 可配置逻辑块 (CLB)
- C2000™ 模数转换器 (ADC) 培训
- C2000™ 增强型脉宽调制器 (ePWM)
- Code Composer Studio™ 快速提示
- 用于优化电源性能的 PCB 布局指南
热门课程
10.3了解高速数据转换器中的信噪比(SNR)和噪声频谱密度(NSD)
大家好!
我叫 Ken Chan, 欢迎观看该演示,
其中将讨论 高速数据
转换器中的 信噪比和
噪声频谱 密度概念。
该演示的第一 部分将通过阐明
信噪比或 SNR 的 含义来详细探究
SNR 的概念。
我们将详细 探究构成
SNR 的噪声 部分的不同分量。
这包括热噪声、 量化噪声和量化
时钟的抖动。
我们将提供抖动 占主导地位的
SNR 的计算示例。
该演示的第二 部分将考察
噪声频谱密度 或 NSD 的概念,
并说明它与 SNR 有何差异。
最后,将提供 一个设计示例,
该示例将重点 说明如何使用
NSD 来估算 DAC 输出的
性能,因为它与 本底噪声相关
性能规格有关。
在实际的系统中, 信号通常会受到
噪声的破坏,这会 导致具有噪声的信号。
简而言之, 信噪比或 SNR
是给定信号带宽中 信号功率与噪声
功率之间的比较。
通常,这可以通过 执行快速傅里叶
变换或 FFT 并 查看频域中的
基波信号功率和本底 噪声功率进行计算。
本底噪声 功率通常
是给定频率 带宽中所有
噪声的积分, 但基波信号
和基波的 谐波除外。
SNR 只不过 是信号功率
与积分本底噪声 功率之间的差异。
由于 SNR 是信号 功率和噪声
功率之间的差异, 因此只能通过
两种方法来增大 SNR。
首先,可以将信号 功率增大至满标度
范围的最大值。
不建议将 输入信号
强度增大至 超过满标度
范围,因为这会对 ADC 的 性能产生不利的影响。
第二种增大 SNR 的 方法是减小噪声功率。
噪声功率 通常是量化
噪声、时钟抖动 导致的噪声、
ADC 孔径抖动 导致的噪声
和电路 热噪声的
组合的结果。
降低这些噪声源之一 或所有这些噪声源
可能有助于 提高 SNR 性能。
假设信号功率 恒定地保持在
固定的水平, 那么可以通过
查看每个信号源的 噪声功率贡献来
估算 SNR。
可以独立对待 每个噪声功率源。
三个不同的 噪声功率源
是量化噪声、 时钟抖动噪声
以及热和 晶体管噪声。
ADC 选择等 设计选择将
包括 N 位的 量化噪声、
ADC 孔径抖动和 ADC 设计的热噪声。
采样时钟选择 将导致时钟
抖动噪声, ADC 的采样率
选择通常 决定噪声的
积分带宽。
通常,这是高达 FS/2 的 第一个奈奎斯特区域。
假设采用 正弦波输入,
可以根据理论 量化误差来计算
量化误差。
这可以表示为 6.02dB/位加 1.76dB。
这决定 N 个 位的最大
可能 SNR。
在实际的 ADC 中, 存在其他限制因素,
如采样时钟 抖动、ADC 孔径
抖动、热噪声、其他 系统噪声源、转换器的
过采样率和 应用信道带宽。
通常有三种 电路噪声源,
即散粒噪声、 闪烁和热噪声。
散粒噪声是由 P-N 结的 直流偏置电流导致的,
该噪声不是恒定的。
它通常具有 白噪声频谱曲线。
闪烁噪声是由有源 电路和电子载体运动
导致的,它通常具有 1/F 的形状,接近于直流。
热噪声是由电阻的 热激励导致的,
它通常具有 白噪声分布。
ADC 中的噪声取决于 输入电阻器的跟踪
保持电路 热噪声贡献,
可将噪声带宽 限制为 RC 带宽。
产生的热噪声 功率可表示为 kT/C。
时钟抖动定义 为时钟边沿
相对于其理想 时间点的随机变化。
该边沿变化将 导致转换器
在非理想时间点 对数据进行采样,
从而导致将增加 总体噪声并影响
SNR 的误差。
抖动导致的 理论 SNR 限制
定义为 -20log(2π*fIN*总抖动)。
总抖动是时钟 源的抖动和
内部 ADC 时钟电路 导致的附加抖动的
组合,该附加抖动 也称为孔径抖动。
时钟抖动将导致 错误的输入波形
样本,输入频率 越高,时钟抖动
越普遍。
可以在抖动对 SNR 的 影响旁边绘制热噪声
对 SNR 的影响。
在低输入频率下, 热噪声处于主导
地位,而在较高的 输入频率下,抖动
导致的噪声 处于主导地位。
可以将产生的 SNR 视为抖动
和热噪声引起的 SNR 损失之和。
右侧的图可用于 说明输入信号的
频率越大,抖动 对它的影响就
越大。
很显然,对于频率 较低的输入,可能的
误差要远 小于频率
较高的输入。
正如前面 提到的,
总抖动是采样 时钟抖动和
孔径抖动的组合。
时钟抖动 是外部采样
时钟源导致的, 可以在相位
噪声分析仪上 进行测量。
孔径抖动发生 在 ADC 时钟电路
内部,无法通过相位 噪声分析仪进行测量。
通常可以使用 非常干净的时钟
和高输入频率 来描述该抖动,
从而根据测量的 SNR 来估算总抖动。
然后,使用测量的 外部采样时钟
相位噪声,可以 获得内部孔径
抖动的估算值。
这是在相位 噪声分析仪上
测量的以 122.88 兆赫兹运行的采样
时钟示例相位噪声图。
抖动是 10 千赫兹至 10 兆赫兹范围内
相位噪声的积分。。
在这种情况下,产生的 抖动是 299 飞秒。
如果相位噪声 图可用,那么
也可以对时钟 源的抖动进行
简单的估算。
在前一个 示例中,10
千赫兹至 10 兆赫兹的
积分相位噪声 为 -75.72dBc/赫兹。
对于等于 122.88 兆赫兹的 fclock,
该公式可得到 299.77 飞秒的抖动。
对于根据抖动 和输入信号
频率进行的 传统 SNR 计算,
还需要考虑 一些注意事项。
在前面,抖动 导致的理论
SNR 限制定义为 总抖动和输入
频率的函数。
不过,这表明 无论采样率
如何,针对某个 输入频率的 SNR
都是相同的。
那么,问题是 过采样具有
什么优点。
为何不为每个 应用使用欠采样?
事实证明, SNR 计算对
采样时钟频率和 输入频率具有
一定的依赖性。
通过将采样 时钟抖动公式
代入到 SNR 公式中, 结果具有两个项。
一个项基于 积分相位噪声,
另一个是 采样频率
基于输入频率 过采样的项。
如果使用过采样, 那么可以通过
该校正项来提高 SNR。
这是用于计算 ADC SNR 的更一般的公式。
该一般公式 很重要,
因为与传统的 公式相比,
它可以对 ADC 的 SNR 性能进行
更好的估算,传统 公式使用抖动对
SNR 的影响的简化估算, 而不考虑采样频率或
输入信号频率。
在大多数情况下, ADC 时钟进行了
良好的滤波,在较大的频率 偏移下具有更好的噪声性能。
在某些情况下, 系统要求通常
限制为特定的 带宽,此时您
只关心特定频带 中的本底噪声性能。
如果使用传统的 SNR 估算方法,则
要求更严格的 噪声规格,
该规格可能是 无法实现的,
或者会使解决方案的 复杂度和成本高于
需要的水平。
通过探究特定 频率和特定
带宽下的 SNR 性能,可以 实现更加优化的系统
解决方案。
我们执行了一个 简单的实验来
验证一般的 ADC SNR 公式。
我们使用了 高速 DAC 来生成
在时钟频率下 具有已知过高
噪声级别的时钟。
这用于驱动 ADC 采样时钟,
向 ADC 发送了两个 不同的输入信号。
一个音调是 10 兆赫兹,另一个
是 100 兆赫兹。
ADC 捕获的生成 信号会进行覆盖
并显示在一起。
不出所料,采样 时钟相位噪声
在 10 兆赫兹 和 100 兆赫兹的
频率下耦合 到输入信号。
过采样校正 因数能够以
25 倍的过采样 率提高 10 兆
赫兹下的相位 噪声性能,从而
使噪声功率 下降 28dB。
此外,在 100 兆 赫兹下,
过采样率为 2.5 倍, 从而导致噪声功率
下降 8dB。
在下一部分中,我们将 讨论 DAC 输出中的本底
噪声概念。
在这里,噪声 频谱密度或
NSD 是针对 SNR 的首选规格。
DAC 的 SNR 估算 方法与 ADC 相同。
类似地,本底 噪声由量化
噪声、时钟和 孔径抖动以及
热和晶体管 噪声构成。
也以相同的方式 对待 SNR 的抖动限制。
对于 DAC,NSD 规格通常比
SNR 更重要。
载波周围的 NSD 的形状
通常必须符合 某种传输掩模。
通常,在需要 SNR 时,系统
往往会使用 带通或低通
滤波器限制 信号的带宽。
然后可以使用 NSD 在滤波器的通带内
估算本底噪声。
这是大多数新 数据表
报告 NSD、针对 SNR 的带宽 限制、第一个奈奎斯特
区域的主要原因。
在实际的系统中, 通常具有某个
针对相关频带的 精密滤波器,
该频带之外的所有 频谱都会被滤除。
它并不报告整个 第一个奈奎斯特
区域的本底 噪声,相反,
显示每赫兹的 本底噪声,然后
估算滤波器的 通带频率内的
本底噪声, 这样更方便。
让我们考虑一个 简单的示例,其中
DAC3484 以 1.2288 千兆个样本/秒的
采样率运行,并在 前 100 兆赫兹内
生成所需的频率。
让我们假设 DAC3484 的 NSD
为 -160dBc/赫兹。
如果使用具有约 FS/2 或第一个
奈奎斯特区域 转角频率的低通
滤波器,并且针对整个 第一个奈奎斯特区域
计算本底噪声,那么 产生的本底噪声是
-72.12dBFS。
不过,如果使用 具有约 100 兆赫兹
转角频率的低通 滤波器,那么 100
兆赫兹内的本底 噪声是 -80dBFS。
如果仅查看 相关的本底
噪声,那么规格 要高大约 8dB。
可以将 NSD 规格转换为
DAC 的 SNR。
NSD 规格是 1 赫兹 bin 的功率。
要将其转换为 特定带宽上的 SNR,
只需将其乘以 赫兹带宽。
如果是典型的 SNR,即在奈奎斯特
区域或 FS/2 上指定,
那么您可以 根据 NSD 然后
添加 10log(FS/2) 来 计算本底噪声。
然后可以从 基波信号功率中
减去本底噪声 以得到 SNR。
对于我们的 实际 DAC3484,
NSD 被指定为 大约每赫兹
-160dBc。
如果 DAC 以 1.25 千兆个 样本/秒的采样率进行
采样,那么本底 噪声计算为
-60dBc/赫兹加s 10log(1.25 千兆赫兹/2)
或 -160dBc 加 88dB, 从而得到 72dBFS 的 SNR。
Fs
总之,ADC 和 DAC 的本底
噪声可以通过 SNR 和 NSD 进行指定。
根据应用,使用 其中一个或另一个
可能会更好。
在决定使用 哪一个时,
最好不要忘记一些 有关 NSD 和 SNR 的要点。
对于整个奈奎斯特 频带上的 SNR,基于
抖动的 SNR 估算 是很便利的估算。
不过,对于带宽受限的 应用而言,这些想法
可能过于乐观。
基于在偏移 频率下测量的
NSD 的 SNR 估算不涉及 接近载波相位噪声,
该噪声可能会影响 百分比 EVM 等带内
测量。
NSD 对于噪声受限的 ACPR 等带外估算而言
很有用。
对于带内和带外 估算而言,将时钟
NSD 曲线和带宽 受限的噪声计算
与用于计算 SNR 的一般 公式结合使用是一种
理想的解决方案。
感谢您观看 本演示。 297
-
 未学习 1.1 数据转换器介绍 - 直流参数
未学习 1.1 数据转换器介绍 - 直流参数
-
 未学习 1.2 数据转换器介绍 - 交流和直流参数
未学习 1.2 数据转换器介绍 - 交流和直流参数
-
 未学习 2.1 数据转换器介绍 - SAR型ADC输入类型
未学习 2.1 数据转换器介绍 - SAR型ADC输入类型
-
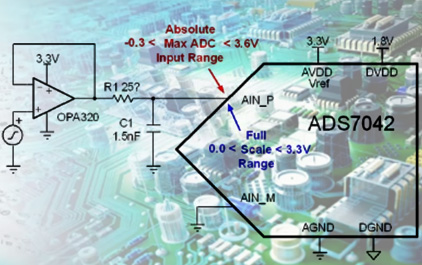 未学习 2.2.1 单端驱动电路分析
未学习 2.2.1 单端驱动电路分析
-
 未学习 2.2.2 反向配置与轨对轨放大器的交越失真
未学习 2.2.2 反向配置与轨对轨放大器的交越失真
-
 未学习 2.3.1 交越失真实验所需硬件软件
未学习 2.3.1 交越失真实验所需硬件软件
-
 未学习 2.3.2 交越失真实验软件设置
未学习 2.3.2 交越失真实验软件设置
-
 未学习 2.3.3 交越失真实验结果
未学习 2.3.3 交越失真实验结果
-
 未学习 2.4.1 仪表放大器输入范围计算
未学习 2.4.1 仪表放大器输入范围计算
-
 未学习 2.4.2 使用软件验证仪表放大器输入共模范围
未学习 2.4.2 使用软件验证仪表放大器输入共模范围
-
 未学习 2.5.1 全差分放大器及失真
未学习 2.5.1 全差分放大器及失真
-
 未学习 2.5.2 全差分驱动电路设计
未学习 2.5.2 全差分驱动电路设计
-
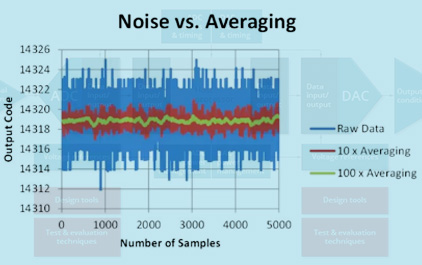 未学习 3.1 误差分析背后的统计学知识
未学习 3.1 误差分析背后的统计学知识
-
 未学习 3.2 理解与校准ADC系统的偏移和增益误差
未学习 3.2 理解与校准ADC系统的偏移和增益误差
-
 未学习 3.3 使用蒙特卡罗SPICE工具进行误差统计分析
未学习 3.3 使用蒙特卡罗SPICE工具进行误差统计分析
-
 未学习 4.1 计算ADC系统的总噪声
未学习 4.1 计算ADC系统的总噪声
-
 未学习 4.2 动手实验-ADC噪声
未学习 4.2 动手实验-ADC噪声
-
 未学习 4.3 ADC 系统中的噪声
未学习 4.3 ADC 系统中的噪声
-
 未学习 4.4 ADC 噪声测量、方法和参数
未学习 4.4 ADC 噪声测量、方法和参数
-
 未学习 4.5 低速 Δ-Σ ADC 的系统噪声性能
未学习 4.5 低速 Δ-Σ ADC 的系统噪声性能
-
 未学习 4.6 分析和计算 ADC 系统中的噪声带宽——多级滤波器
未学习 4.6 分析和计算 ADC 系统中的噪声带宽——多级滤波器
-
 未学习 4.7 分析和计算 ADC 系统中的噪声带宽——数字滤波器
未学习 4.7 分析和计算 ADC 系统中的噪声带宽——数字滤波器
-
 未学习 4.8 增益对噪声、ADC FSR 和动态范围的影响
未学习 4.8 增益对噪声、ADC FSR 和动态范围的影响
-
 未学习 4.9 计算放大器 + ADC 总噪声:设计示例
未学习 4.9 计算放大器 + ADC 总噪声:设计示例
-
 未学习 4.10 ADC 系统中的参考噪声简介
未学习 4.10 ADC 系统中的参考噪声简介
-
 未学习 4.11 参考噪声对信号链性能的影响
未学习 4.11 参考噪声对信号链性能的影响
-
 未学习 4.12 降低参考噪声
未学习 4.12 降低参考噪声
-
 未学习 5.1 频域介绍
未学习 5.1 频域介绍
-
 未学习 5.2 快速傅立叶变换及加窗函数
未学习 5.2 快速傅立叶变换及加窗函数
-
 未学习 5.3 改善频率指标的方法:相干采样及滤波
未学习 5.3 改善频率指标的方法:相干采样及滤波
-
 未学习 5.4 混叠及抗混叠滤波器
未学习 5.4 混叠及抗混叠滤波器
-
 未学习 5.5 实验 - 混叠和抗混叠滤波器
未学习 5.5 实验 - 混叠和抗混叠滤波器
-
 未学习 6.1 SAR ADC及其器件选型
未学习 6.1 SAR ADC及其器件选型
-
 未学习 6.2 驱动放大器的选型和验证
未学习 6.2 驱动放大器的选型和验证
-
 未学习 6.3 建立SAR ADC的仿真模型
未学习 6.3 建立SAR ADC的仿真模型
-
 未学习 6.4 如何计算RC滤波器的值
未学习 6.4 如何计算RC滤波器的值
-
 未学习 6.5 最终的仿真验证
未学习 6.5 最终的仿真验证
-
 未学习 6.6 滤波器RC选型的理论计算方法
未学习 6.6 滤波器RC选型的理论计算方法
-
 未学习 6.7 R-C组件选择背后的数学
未学习 6.7 R-C组件选择背后的数学
-
 未学习 7.1 电压基准概述
未学习 7.1 电压基准概述
-
 未学习 7.2 参考驱动器拓扑概述
未学习 7.2 参考驱动器拓扑概述
-
 未学习 7.3 了解SAR参考输入模型
未学习 7.3 了解SAR参考输入模型
-
 未学习 7.4 开发SAR输入参考模型
未学习 7.4 开发SAR输入参考模型
-
 未学习 7.5 驱动参考实验
未学习 7.5 驱动参考实验
-
 未学习 7.6 ADC:SAR 基准输入 - CDAC
未学习 7.6 ADC:SAR 基准输入 - CDAC
-
 未学习 8.1 SAR ADC功率调节
未学习 8.1 SAR ADC功率调节
-
 未学习 8.2 动手实验 - 系统功率调节
未学习 8.2 动手实验 - 系统功率调节
-
 未学习 9.1 EOS和ESD
未学习 9.1 EOS和ESD
-
 未学习 9.3 向TINA 导入二极管PSpice模型
未学习 9.3 向TINA 导入二极管PSpice模型
-
 未学习 9.4 通过高压放大器保护低压ADC
未学习 9.4 通过高压放大器保护低压ADC
-
 未学习 9.5 保护低压ADC-改进的解决方案
未学习 9.5 保护低压ADC-改进的解决方案
-
 未学习 9.6 用TVS二极管保护ADC
未学习 9.6 用TVS二极管保护ADC
-
 未学习 9.7 用TVS二极管保护ADC –改进的解决方案
未学习 9.7 用TVS二极管保护ADC –改进的解决方案
-
 未学习 10.1 了解和比较高速模数(ADC)和数模转换器(DAC)转换器架构
未学习 10.1 了解和比较高速模数(ADC)和数模转换器(DAC)转换器架构
-
 未学习 10.2 抖动对高速模数转换器(ADC)信噪比(SNR)的影响
未学习 10.2 抖动对高速模数转换器(ADC)信噪比(SNR)的影响
-
 未学习 10.3了解高速数据转换器中的信噪比(SNR)和噪声频谱密度(NSD)
未学习 10.3了解高速数据转换器中的信噪比(SNR)和噪声频谱密度(NSD)
-
 未学习 10.4 带宽与频率 - 子采样概念
未学习 10.4 带宽与频率 - 子采样概念
-
 未学习 10.5 高速数据转换器中的采样率与数据速率,抽取(DDC)和插值(DUC)概念
未学习 10.5 高速数据转换器中的采样率与数据速率,抽取(DDC)和插值(DUC)概念
-
 未学习 10.6 频率和采样率规划:了解高速ADC中的采样,奈奎斯特区,谐波和杂散性能
未学习 10.6 频率和采样率规划:了解高速ADC中的采样,奈奎斯特区,谐波和杂散性能
-
 未学习 10.7 高速数据转换器信号处理:真实和复杂的调制
未学习 10.7 高速数据转换器信号处理:真实和复杂的调制
-
 未学习 (中文)11.1 ADC 系统中的噪声
未学习 (中文)11.1 ADC 系统中的噪声
-
 未学习 (中文)11.3 ADC 噪声测量、方法和参数
未学习 (中文)11.3 ADC 噪声测量、方法和参数
-
 未学习 (中文)11.4 低速 Δ-Σ ADC 的系统噪声性能
未学习 (中文)11.4 低速 Δ-Σ ADC 的系统噪声性能
-
 未学习 (中文)11.5 分析和计算 ADC 系统中的噪声带宽——多级滤波器
未学习 (中文)11.5 分析和计算 ADC 系统中的噪声带宽——多级滤波器
-
 未学习 (中文)11.6 分析和计算 ADC 系统中的噪声带宽——数字滤波器
未学习 (中文)11.6 分析和计算 ADC 系统中的噪声带宽——数字滤波器
-
 未学习 (中文)11.7 增益对噪声、ADC FSR 和动态范围的影响
未学习 (中文)11.7 增益对噪声、ADC FSR 和动态范围的影响
-
 未学习 (中文)11.8 计算放大器 + ADC 总噪声:设计示例
未学习 (中文)11.8 计算放大器 + ADC 总噪声:设计示例
-
 未学习 (中文)11.9 ADC 系统中的参考噪声简介
未学习 (中文)11.9 ADC 系统中的参考噪声简介
-
 未学习 (中文)11.10 参考噪声对信号链性能的影响
未学习 (中文)11.10 参考噪声对信号链性能的影响
-
 未学习 (中文)11.11 降低参考噪声
未学习 (中文)11.11 降低参考噪声
-
 未学习 动手实验:放大器稳定和电荷桶滤波器设计
未学习 动手实验:放大器稳定和电荷桶滤波器设计
-
 未学习 无需放大器即可驱动 SAR ADC
未学习 无需放大器即可驱动 SAR ADC
-
 未学习 外部EOS保护装置
未学习 外部EOS保护装置
-
 未学习 (中文)5.5 实验 - 混叠和抗混叠滤波器
未学习 (中文)5.5 实验 - 混叠和抗混叠滤波器
-
 未学习 (中文)6.7 R-C组件选择背后的数学
未学习 (中文)6.7 R-C组件选择背后的数学
-
 未学习 (中文)7.1 电压基准概述
未学习 (中文)7.1 电压基准概述
-
 未学习 (中文)7.3 SAR 基准输入 - CDAC
未学习 (中文)7.3 SAR 基准输入 - CDAC
-
 未学习 (中文)7.4 了解SAR参考输入模型
未学习 (中文)7.4 了解SAR参考输入模型
-
 未学习 (中文)7.5 开发SAR输入参考模型
未学习 (中文)7.5 开发SAR输入参考模型
-
 未学习 (中文)7.6 驱动参考实验
未学习 (中文)7.6 驱动参考实验
-
 未学习 (中文)8.1 SAR ADC功率调节
未学习 (中文)8.1 SAR ADC功率调节
-
 未学习 (中文)8.2 动手实验 - 系统功率调节
未学习 (中文)8.2 动手实验 - 系统功率调节
-
 未学习 (中文)9.1 EOS和ESD
未学习 (中文)9.1 EOS和ESD
-
 未学习 (中文)9.3 向TINA 导入二极管PSpice模型
未学习 (中文)9.3 向TINA 导入二极管PSpice模型
-
 未学习 (中文)9.4 通过高压放大器保护低压ADC
未学习 (中文)9.4 通过高压放大器保护低压ADC
-
 未学习 (中文)9.5 保护低压ADC-改进的解决方案
未学习 (中文)9.5 保护低压ADC-改进的解决方案
-
 未学习 (中文)9.6 用TVS二极管保护ADC
未学习 (中文)9.6 用TVS二极管保护ADC
-
 未学习 (中文)9.7 用TVS二极管保护ADC –改进的解决方案
未学习 (中文)9.7 用TVS二极管保护ADC –改进的解决方案
-
 未学习 (中文)10.1 了解和比较高速模数(ADC)和数模转换器(DAC)转换器架构
未学习 (中文)10.1 了解和比较高速模数(ADC)和数模转换器(DAC)转换器架构
-
 未学习 (中文)10.2 抖动对高速模数转换器(ADC)信噪比(SNR)的影响
未学习 (中文)10.2 抖动对高速模数转换器(ADC)信噪比(SNR)的影响
-
 未学习 (中文)10.3 了解高速数据转换器中的信噪比(SNR)和噪声频谱密度(NSD)
未学习 (中文)10.3 了解高速数据转换器中的信噪比(SNR)和噪声频谱密度(NSD)
-
 未学习 (中文)10.4 带宽与频率 - 子采样概念
未学习 (中文)10.4 带宽与频率 - 子采样概念
-
 未学习 (中文)10.5 高速数据转换器中的采样率与数据速率,抽取(DDC)和插值(DUC)概念
未学习 (中文)10.5 高速数据转换器中的采样率与数据速率,抽取(DDC)和插值(DUC)概念
-
 未学习 (中文)10.6 频率和采样率规划:了解高速ADC中的采样,奈奎斯特区,谐波和杂散性能
未学习 (中文)10.6 频率和采样率规划:了解高速ADC中的采样,奈奎斯特区,谐波和杂散性能
-
 未学习 (中文)10.7 高速数据转换器信号处理:真实和复杂的调制
未学习 (中文)10.7 高速数据转换器信号处理:真实和复杂的调制
-
 未学习 (中文)了解 ADC 系统中的电源噪声
未学习 (中文)了解 ADC 系统中的电源噪声
-
 未学习 (中文)时钟噪声如何影响精密 ADC 测量
未学习 (中文)时钟噪声如何影响精密 ADC 测量
-
 未学习 (中文)电源噪声降低技术
未学习 (中文)电源噪声降低技术